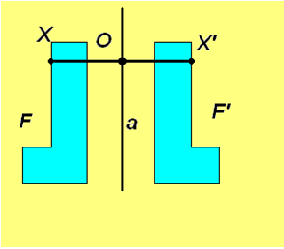
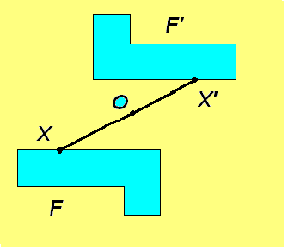
Симметрия в теории и на практике

Главная страница	МатематикА	Основные разделы
История симметрии	Симметрия относительно точки Симметрия относительно точки (центральная симметрия) – это преобразование фигуры F в фигуру F’, при котором каждая её точка X переходит в точку X’, симметричную относительно данной точки O. Симметрия относительно прямой Симметрия относительно прямой (осевая симметрия) – это преобразование фигуры F в фигуру F’, при котором каждая её точка X переходит в точку X’, симметричную относительно данной прямой a. Теория симметричных многочленов Многочлен от x и y называют симметричным, если он не изменяется при замене x на y, а y на x . Приведём важнейшие примеры симметричных многочленов. Как известно из арифметики, при перестановке мест слагаемых сумма не меняется, т. е: x + y = y + x Теория симметрических многочленов очень проста и к тому же позволяет решать многие алгебраические задачи: решение иррациональных уравнений, доказательство тождеств и неравенств, разложение на множители, решение систем алгебраических уравнений, и т. д. С помощью теории симметрических многочленов решение этих задач заметно упрощается и, что самое главное, проводится стандартным приёмом.	Буридановский осел
Симметрия сайта		Треугольник Паскаля
Аннотация к сайту		Круги на полях

donleonchik@yandex.ru Москва, 2009г.